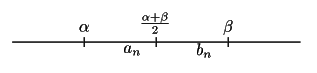![]() より
より
つまり
でも,「はさみうちの原理」というにしては簡単すぎるし,これで証明になっているのでしょうか.
南海 ともすればこのように考えやすいが,これは「はさみうちの原理」の証明としては不完全だ.
一般に,極限の入った等号![]() は何を意味しているのかといえば
は何を意味しているのかといえば
ということだ.
史織
すると,私の証明では,数列![]() が収束すること,極限の存在の証明が抜けているのですね.
が収束すること,極限の存在の証明が抜けているのですね.
でもそれはどのようにして示せばよいのですか.
南海
そういうときは「定義にかえれ」だ.数列![]() が値
が値![]() に収束するとはどういうことか.
に収束するとはどういうことか.
史織
「![]() が大きくなれば
が大きくなれば![]() の値が
の値が![]() に近づく」ということです.
に近づく」ということです.
南海 「近づく」というのはどういうことか.
史織 「数直線上の距離が小さくなる」,ですか?
南海
そうだ.つまり![]() がいくらでも小さくなるということが,
数列
がいくらでも小さくなるということが,
数列![]() が値
が値![]() に収束するということの定義だ.
に収束するということの定義だ.
史織 でも,「いくらでも小さくなる」が「0に収束する」ということなら, 「収束」を定義するのに「収束」を用いたことにはなりませんか.
南海 うーん.それは鋭い質問だ.「いくらでも小さくなる」といったあいまいな言葉を使わずに 収束することを定義しなければならない. いろんな人もこのようなことを考えた.そこで考え出されたのが次のような定義だ. これは「実数の連続性と代数学の基本定理」で同じことが言われているのだが,改めて 数列「収束」を定義しよう.
数列![]() と数
と数![]() がある.
任意の正の実数
がある.
任意の正の実数![]() に対して,番号
に対して,番号![]() で
で
![]() であるすべての
であるすべての![]() について
について
![]()
となるものが存在するとき,
![]() が
存在し,極限値が
が
存在し,極限値が![]() であると定める.
であると定める.
「任意の正の実数![]() に対して,番号
に対して,番号![]() で…となるものが存在」というところは
「どのような小さい」正の実数
で…となるものが存在」というところは
「どのような小さい」正の実数![]() が指定されても,それに対して,「つねに」番号
が指定されても,それに対して,「つねに」番号![]() が存在する,
ということなのだ.そのような副詞を省いて論理の骨子で言うと先のようになるのだ.
が存在する,
ということなのだ.そのような副詞を省いて論理の骨子で言うと先のようになるのだ.
この定義がわかりにくいときは例で考える.数列![]() を
を
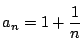 とする.
これはもちろん1に収束する.
とする.
これはもちろん1に収束する.![]() を
を
![]() にして,ある番号
にして,ある番号![]() より大きい番号では
より大きい番号では
史織
(少し考え)![]() ですね.そうか,
ですね.そうか,
![]() より小さくしたければ
より小さくしたければ![]() だ,
どんなに小さい
だ,
どんなに小さい![]() でも,つねに番号
でも,つねに番号![]() は存在しますね.
は存在しますね.
では,
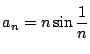 も1に収束しますが,
も1に収束しますが,
南海
いろいろ考えるな.一般には具体的に![]() を求めるのは簡単でない.
を求めるのは簡単でない.
史織
実際に![]() を求めるということではなく,
を求めるということではなく,![]() が存在するということで,「収束」を定義するのですね.
が存在するということで,「収束」を定義するのですね.
この「収束」の定義って「いくらでも」とか「近づく」とかのよくわからない言葉が入っていませんね.
南海 そうなのだ.
その代わりに「任意の」という論理の言葉が入る.これがいわゆる
![]() 論法というもので,
大学初年に習う解析の最初の関門だが,このように考えれば自然な発想であることがわかる.
論法というもので,
大学初年に習う解析の最初の関門だが,このように考えれば自然な発想であることがわかる.
史織
今は![]() ではなく
ではなく![]() でしたが.
でしたが.
南海
![]() 論法は次のように
論法は次のように
![]() を定義する.
を定義する.
関数![]() と数
と数![]() がある.
任意の正の実数
がある.
任意の正の実数![]() に対して,正の実数
に対して,正の実数![]() で
で
![]() である
である![]() について
について
![]()
となるものが存在するとき,極限
![]() が存在し
極限値が
が存在し
極限値が![]() であると定める.
であると定める.
史織 これもわかります.
南海
いずれにせよ,このような厳密な定義があるということを知ったうえで,
数列![]() が数
が数![]() に収束するとは,
に収束するとは,
![]() が大きくなるとき,絶対値
が大きくなるとき,絶対値![]() がいくらでも小さくなることと理解すればよい.
がいくらでも小さくなることと理解すればよい.
この定義のもとではさみうちの原理を証明しよう.
条件![]() のもとで,
のもとで,![]() がいくらでも小さくなることを示せばよい.
がいくらでも小さくなることを示せばよい.
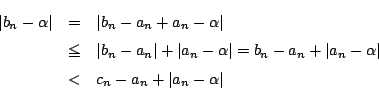
よって数列![]() は
は![]() に収束する.つまり
に収束する.つまり
史織 三角不等式ですか.
南海
そう.そこで注意を一つ.
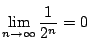 なのではさみうちの原理によって
なのではさみうちの原理によって
はさみうちの原理は
![]() のいずれもが定数でないときに両方が同じ値に収束すれば,
のいずれもが定数でないときに両方が同じ値に収束すれば,
![]() も収束してその極限値が
も収束してその極限値が![]() であることを示すものである.これはしっかりと押さえておきたい.
であることを示すものである.これはしっかりと押さえておきたい.
南海 せっかく収束を厳密に考えたのだから,次のことも示しておこう.
2つの数列
![]() がすべての
がすべての![]() で
で![]() を満たし,各々が収束すれば
を満たし,各々が収束すれば
史織
それぞれの極限を
![]() とする.
とする.![]() であると仮定する.
であると仮定する.
![]() より小さい
より小さい![]() をとる.
をとる.![]() が存在して
が存在して![]() に対して
に対して
![]() ,
,
![]() となる.
となる.
このとき図のように![]() なので,条件と矛盾した.
なので,条件と矛盾した.
南海 これでよい.